1 信息与信息熵
信息:在计算机科学中,我们通常认为信息是一种数据或指令的集合,泛指我们通过载体传播的内容。
信息量:对信息的度量,一般用bit。香农对信息量计算公式如下
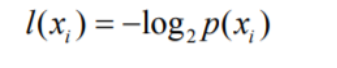
信息熵:1948年,香农提出了“信息熵”的概念,解决了对信息的量化度量问题,即有多少信息。“信息熵”是香农从热力学“热熵”(表示分子状态混乱程度的物理量)借用过来,熵是形容物质混乱程度的单位,当物质混乱程度越高的时候熵值越高。信息熵就是信息中排除冗余后的平均信息量。
香农公式(信息熵计算公式):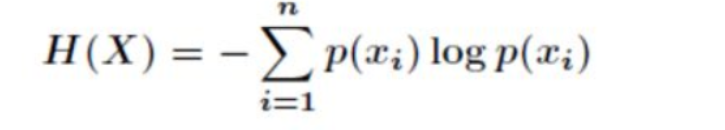
信息熵的应用:信息熵目前被广泛应用在各种压缩场景种,对于长度相同的信息,熵值p越大,则表明信息内容越有规律,可压缩的体积就越大;p越小,则信息内容越随机,可压缩的体积就越小。
2 信息熵公式解析
2.1 信息量公式解析
黑箱子有8个红色球,1个黑色球。随机抽取一个,每个球被抽中的概率相同,但是抽中红色球概率更高一些。
当抽中黑色球,看到黑色球时,我们获取到的信息量远远比抽中红色球多得多。
越小概率发生的事情,其产生的信息量越大。
在电报通信中,经常使用的英文字母E可以使用一个”.”来表示,出现叫较少的Q,X,Z 等则使用更多的点和破折号来表示。可以最大程度节省信道容量,传输时间会更少。
信息量公式条件如下:
- 概率增大而信息减少
- 函数值大于等于0
香农最后选择了对数函数,以2为底,符合二进制位。
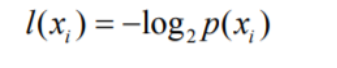
以上文抽球为例,随机抽取一个,抽中红色球的概率是7/8,抽中黑色球的概率是1/8。
红色球信息量:-log2(7/8)=1.93
黑色球信息量:-log2(1/8)=3.00
再举一个例子:
比如8个球,红球是4个,黑球是2个,白球是2个,那么对应的概率就是1/2 1/4 1/4
红球信息量:-log2(1/2)=1
黑球信息量:-log2(1/4)=2
白球信息量:-log2(1/4)=2
那么在信道里传输的时候,就可以用1bit的符号代表红色,用2bit的符号代表黑色和白色球。
那么三种球,数学期望是多少呢?可以用多少bit“平均”代表三种球呢?
数学期望(期望值是指在一个离散性随机变量试验中每次可能结果的概率乘以其结果值之后的累加和)计算如下:
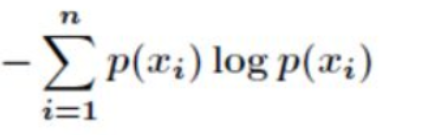
H(X)=1/2*1+1/4*2+1/4*2=1.5,用1.5bit来代表“平均值”,即数学期望
也用这种方式来表示“信息熵”
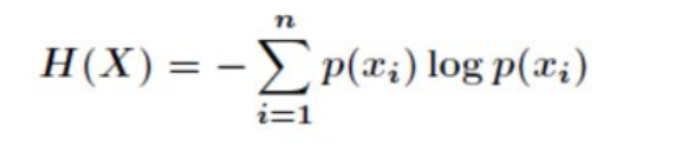
信息熵越大,代表数学期望越高,“期望bit”越大,概率小的字符出现的次数就多,所获得的信息量越多,说明信息越复杂。
3 信息熵在恶意代码分析中的应用
有一个IDA插件idatropy
https://yunyawu.com/2021/07/01/ida%E6%8F%92%E4%BB%B6%EF%BC%9Aidatropy/
能直观绘画出各个段的熵值图。
如果发现哪个段,熵值突变,就有可能有很多违反常规的数据,就要仔细观察分辨。

